Yonsei University (Mirae Campus)
Scientific Computing and Machine Learning Lab
Scientific Computing and Machine Learning
Welcome to our research lab, where we harness the power of scientific computing and scientific machine learning to tackle challenging problems spanning computational physics and medicine. Our team is dedicated to developing state-of-the-art numerical solvers and innovative deep learning methods aimed at improving performance and efficiency. By combining physics-based simulation with modern ML approaches, we push the frontiers of predictive modeling, enabling faster and more accurate solutions to real-world challenges. Our interdisciplinary projects bring together experts in applied mathematics, computational science, data science, and engineering, creating a collaborative environment that fosters cutting-edge research and impactful discoveries. We invite you to explore our work and join us on our journey toward scientific and technological breakthroughs. If you’re interested in learning more about our research group or would like to get involved in our projects, please feel free to reach out via email at mshin@yonsei.ac.kr.
Research Statement
Scientific Computing
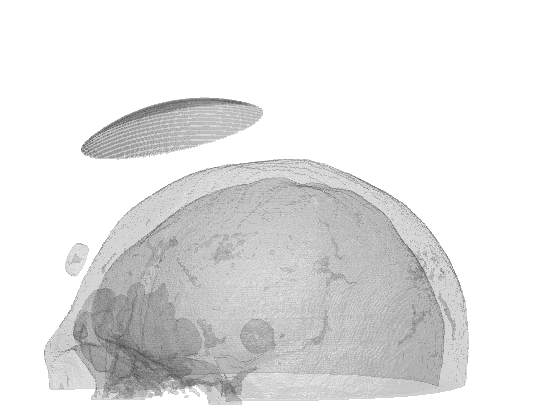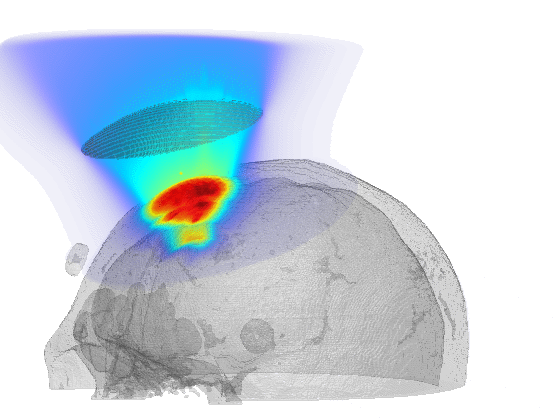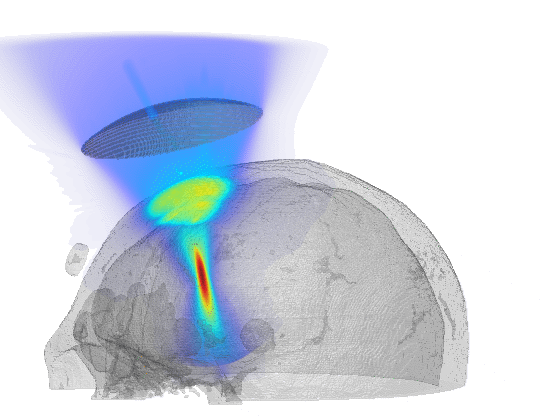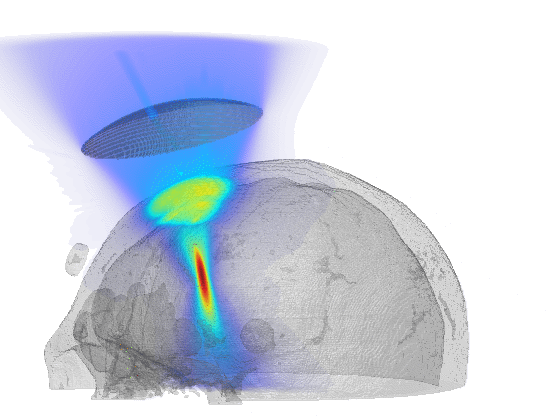
Scientific computing in computational physics and medicine lies at the intersection of advanced numerical methods, high-performance computing, and robust data analysis tools. In computational physics, researchers employ these techniques to model and simulate a wide range of phenomena governed by partial differential equations, such as radiation transport, gas dynamics, fluid flows, electromagnetic fields, and quantum mechanical systems. By developing specialized algorithms and utilizing state-of-the-art hardware, scientists are able to explore complex physical processes that would be too costly, dangerous, or simply impossible to study through traditional experimentation. These insights not only push the boundaries of fundamental research but also guide practical applications in engineering, energy production, and environmental science.
In the medical domain, scientific computing paves the way for more accurate diagnostics, personalized treatment plans, and improved patient outcomes. By creating computational models of biological processes—from tissue mechanics to molecular interactions—researchers can investigate how diseases progress and how patients respond to different therapies. Advanced imaging techniques or numerical simulation techniques coupled with machine learning methods enhance the resolution or the accuracy of these models, helping clinicians identify critical markers of disease earlier and more reliably or predict treatment outcomes. Through interdisciplinary collaboration between computer scientists, physicists, and medical professionals, scientific computing plays an increasingly pivotal role in transforming both patient care and our broader understanding of human health.
Scientific Machine Learning

Scientific machine learning (SciML) is a rapidly growing field that integrates the rigor of scientific modeling with the adaptability of modern machine learning techniques. Unlike conventional data-driven methods, SciML leverages domain-specific knowledge—such as physical laws, governing equations, and structural relationships—in the development of learning algorithms. This combination leads to models that are both accurate and interpretable, helping researchers overcome limitations commonly faced when relying solely on purely empirical approaches. For instance, incorporating physics-based constraints into neural networks or including partial differential equation solvers in learning pipelines can reduce the amount of data required and improve model robustness in the face of noisy or incomplete measurements.
A key strength of scientific machine learning lies in its ability to bridge computational science and real-world applications, from computational physics to biomedical engineering. By embedding deep learning methods within established numerical solvers, scientists can accelerate simulations while maintaining high levels of accuracy. Furthermore, advanced features such as uncertainty quantification help practitioners gauge model confidence and guide the design of future experiments or treatment strategies. This interdisciplinary synergy between machine learning and traditional scientific modeling is driving innovation across various domains, ultimately enabling more efficient, interpretable, and impactful scientific discoveries.
Surrogate Modeling

Surrogate modeling is a technique used in computational science and engineering to approximate the behavior of complex systems with simpler, more efficient models. Rather than solving expensive, high-fidelity simulations repeatedly—such as those arising from physics-based partial differential equations—researchers develop “surrogate” or “meta” models that closely mimic the response of the original system at a fraction of the computational cost. These surrogate models are typically trained on a set of input-output data generated by the high-fidelity solver; by learning the underlying patterns, they can provide fast predictions for new inputs without running the full simulation.
A key advantage of surrogate modeling is its ability to enable more extensive exploration of parameter spaces and support advanced tasks like optimization, sensitivity analysis, and uncertainty quantification. In many real-world scenarios—like the design of nuclear reactors, jet engines or patient-specific medical treatments—performing numerous full-scale simulations can be prohibitively time-consuming or expensive. Surrogate models help researchers overcome these limitations by reducing computational overhead while preserving essential accuracy. As computational resources continue to expand and machine learning algorithms become more sophisticated, the role of surrogate modeling in accelerating scientific discovery and engineering design is poised to grow even further.